建立时序关系
在Transformer中,我们希望建立token之间的时序关系。但是由于Attention:
$$
Attention(Q,K,V) = softmax(\frac{Q K^T}{\sqrt{d_k}})V
$$
在token上是全对称的,也就是$f(\mathbf{x}, \mathbf{y}) = f(\mathbf{y}, \mathbf{x})$。因此,我们需要位置编码来引入时序关系:
$$
f(\mathbf{x} + \mathbf{p}_m, \mathbf{y} + \mathbf{p}_n) != f(\mathbf{y} + \mathbf{p}_m, \mathbf{x} + \mathbf{p}_n)
$$
构建位置编码
我们的位置编码有三个目标:
- 去除Attention的全对称关系。
- 引入时序关系。
- 距离遗忘。(距离远的token,位置向量内积值要小)
注意力内积
Attention其实是计算两个向量之间的内积来作为注意力权重。因此,加上位置编码后,$\mathbf{x}$与$\mathbf{y}$的内积为:
$$
\begin{equation}
<\mathbf{x} + \mathbf{p}_m, \mathbf{y} + \mathbf{p}_n> = <\mathbf{x}, \mathbf{y}> + <\mathbf{x}, \mathbf{p}_n> + <\mathbf{y}, \mathbf{p}_m> + <\mathbf{p}_m, \mathbf{p}_n> \\ = \mathbf{x}^T \mathbf{y} + \mathbf{x}^T \mathbf{p}_n + \mathbf{y}^T \mathbf{p}_m + \mathbf{p}_m^T \mathbf{p}_n
\label{eq:0}
\end{equation}
$$
$\mathbf{x}^T \mathbf{p}_n + \mathbf{y}^T \mathbf{p}_m$这一项代表是自身向量在其他位置的位置向量的映射,它与自身向量的大小和方向有关,不是与位置唯一相关。$\mathbf{p}_m^T \mathbf{p}_n$则是两个位置的位置向量内积,与位置唯一相关。
将位置编码视为扰动
视为扰动的思路来自苏神博客。
如果我们认为$\mathbf{p} << \mathbf{x}$,$f(\mathbf{x} + \mathbf{p}_m, \mathbf{y} + \mathbf{p}_n)$可以在$\mathbf{x}$和$\mathbf{y}$处泰勒展开来做二阶的近似:
$$
\begin{equation}
f(\mathbf{x} + \mathbf{p}_m, \mathbf{y} + \mathbf{p}_n) \approx f(\mathbf{x}, \mathbf{y}) + \mathbf{p}_m^T \nabla_x f + \mathbf{p}_n^T \nabla_y f + \\ \frac{1}{2}( \mathbf{p}_m^T H_x \mathbf{p}_m + \mathbf{p}_n^T H_y \mathbf{p}_n + 2 \mathbf{p}_m^T H_{xy} \mathbf{p}_n ) \\
= f(\mathbf{x}, \mathbf{y}) + \mathbf{p}_m^T \nabla_x f + \mathbf{p}_n^T \nabla_y f + \\ \frac{1}{2}\mathbf{p}_m^T H_x \mathbf{p}_m + \frac{1}{2} \mathbf{p}_n^T H_y \mathbf{p}_n + \mathbf{p}_m^T H_{xy} \mathbf{p}_n
\
\label{eq:1}
\end{equation}
$$
当$H_{xy}=I$时,\eqref{eq:1}可以与“注意力内积”部分有类似的结论。
ALiBi位置编码
\eqref{eq:0}可以很自然地改写为:
$$
\begin{equation}
<\mathbf{x} + \mathbf{p}_m, \mathbf{y} + \mathbf{p}_n> = <\mathbf{x}, \mathbf{y}> + \mathbf{x}^T \mathbf{p}_n + \mathbf{y}^T \mathbf{p}_m + \mathbf{p}_m^T \mathbf{p}_n \\
\approx <\mathbf{x}, \mathbf{y}> + \mathbf{p}_m^T \mathbf{p}_n = <\mathbf{x}, \mathbf{y}> + \mathbf{P}
\label{eq:2}
\end{equation}
$$
为了实现位置编码的三个目标。ALiBi编码采用了最朴素的方法,其实也最符合一拍脑袋就想到的直觉:用位置的序号差来构成位置编码矩阵$\mathbf{P}$,再乘以一个权重$m$来调整数值大小。但是我不清楚这样的方式是否会距离遗忘的特性,似乎仅满足了前两个目标。
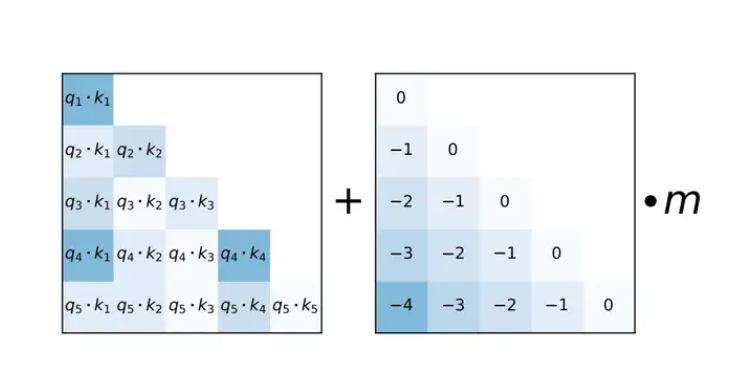
ALiBi位置编码
Sinusoidal位置编码
Sinusodial位置编码在Transformer开山论文中提出:
$$
\begin{cases}
\mathbf{p}_{k,2i} = sin(\frac{k}{10000^{2i/d}}) \\
\mathbf{p}_{k,2i+1} = cos(\frac{k}{10000^{2i/d}})
\end{cases}
$$
接下来我们将推导上面的式子:
为了推导便利,我们假设$\mathbf{p}_m$和$\mathbf{p}_n$的维度为2。我们希望$\mathbf{p}_m^T \mathbf{p}_n$满足下面的条件:
$$
\begin{cases}
\underbrace{\mathbf{p}_m^T \mathbf{p}_n = f(m-n)}_\text{希望能表示相对位置} \\
\underbrace{\mathbf{p}_m^T \mathbf{p}_n = 0, \quad |m - n| >> 0}_\text{距离越远的token,编码越接近0,具有遗忘能力}
\end{cases}
$$
当$m=n时$,$||\mathbf{p}_m||^2 = f(0) = 1$。我们这里设
$$
\mathbf{p}_m =
\left[
\begin{array}{c}
x \\ y
\end{array}
\right]
$$
那么可以得到$x^2 + y^2 = 1$,在坐标平面上是一个圆。
既然位置向量都在单位圆上,那么说明单位向量的不同旋转角度代表了不同的位置。所以不妨我们改写为极坐标系($r=1$):
$$
\mathbf{p}_m =
\left[
\begin{array}{c}
cos\theta_m \\ sin\theta_m
\end{array}
\right]
$$
$$
\mathbf{p}_m^T \mathbf{p}_n = cos\theta_m cos\theta_n + sin\theta_m sin\theta_n = cos(\theta_n - \theta_m) = cos(a(n-m))
$$
当我们考虑更高维度时:
$$
\mathbf{p}_m =
\left[
\begin{array}{c}
cos \theta_{m,0} \\ sin\theta_{m,0} \\ \vdots \\ cos \theta_{m,[d/2]-1} \\ sin\theta_{m,[d/2] - 1}
\end{array}
\right]
$$
$$
\mathbf{p}_m^T \mathbf{p}_n = \sum_{i=0}^{[d/2] - 1} cos(f(\frac{2i}{d})(n-m))
$$
为什么是$f(\frac{2i}{d})$?因为$\frac{2i}{d} \in [0, 1)$,这样便于改为积分的形式:
$$
\mathbf{p}_m^T \mathbf{p}_n = \frac{d} {2} \sum_{i=0}^{[d/2] - 1} cos(f(\frac{2i}{d})(n-m)) \frac{2}{d} \\
= \frac{d} {2} \int_{0}^{1} cos(f(t)(n-m)) dt
$$
至于$f(t)$函数如何确认,请转到这里。我们直接对Transformer给出的$f(t)=\frac{1}{10000^{t}}$代入,然后可视化得到下面的图:
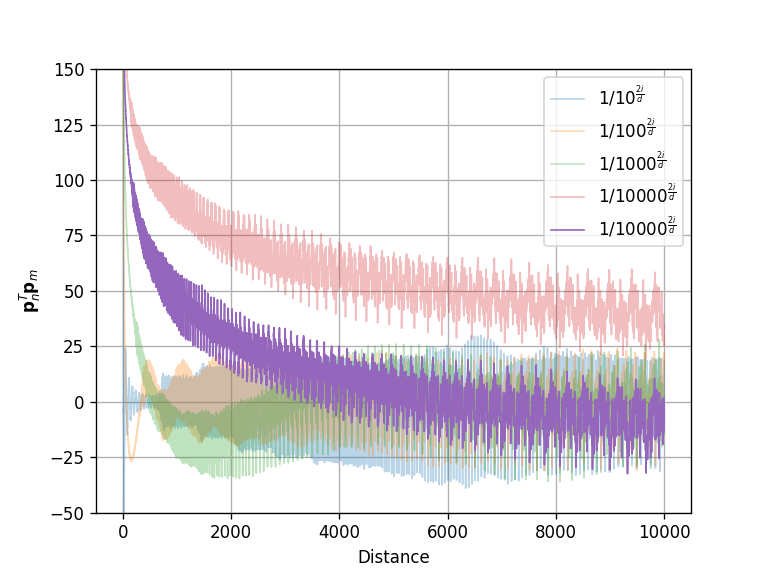
对于底数的分析
可以发现,当$f(t)=\frac{1}{10000^{t}}$时,$\mathbf{p}_m^T \mathbf{p}_n$满足了我们提到的三个目标。重要的是第三个目标,当距离很大时,距离向量内积接近0。


